Tobias Blickhan

📄 MRX on arXiv 📊 Poster 💻 Code

In a fusion device operating near steady state, the plasma can be modeled as being in magnetohydrostatic (MHS) equilibrium. Finding such equilibria is crucial for designing and operating fusion devices. The equilibrium configuration determines properties such as stability and confinement, and reconstruction of equilibria from diagnostic measurements is essential for control.

In a domain $\Omega \subset \mathbb{R}^3$, the MHS equations are:

\[(\text{curl } B) \times B - \nabla p = 0 \quad \text{and} \quad \text{div } B = 0\]

together with appropriate boundary conditions. Here, $B$ is the magnetic field and $p$ the plasma pressure. This is inherently a three-dimensional problem, which makes it computationally challenging.

Most established methods (VMEC, DESC) simplify the search for equilibria to configurations with nested flux surfaces. However, relevant configurations in experiments feature magnetic islands and chaotic regions, violating this assumption.

Magnetic relaxation provides an opportunity to solve for very general equilibrium solutions. These methods rely on the observation that MHS states are stationary points of a constrained optimization process.

The MRX code is easy to use – just clone and pip install it!

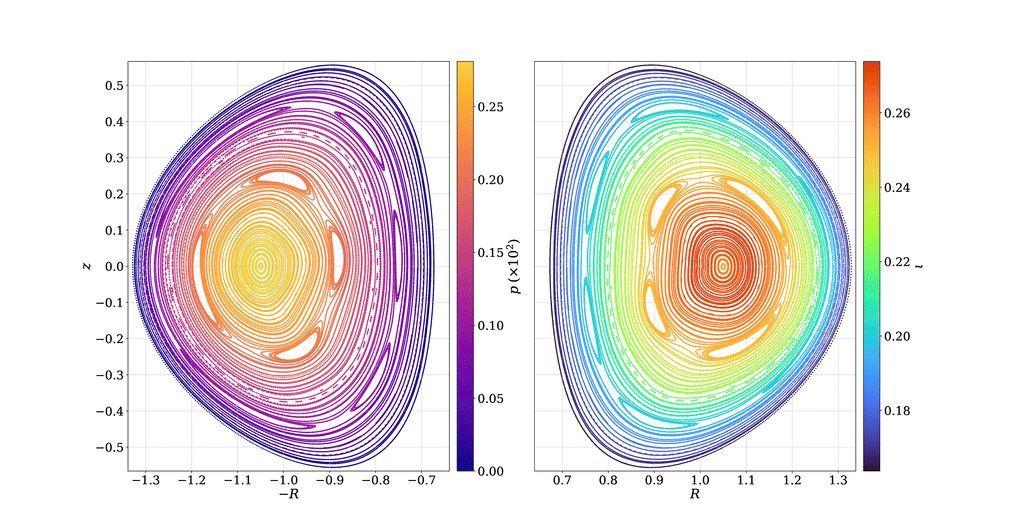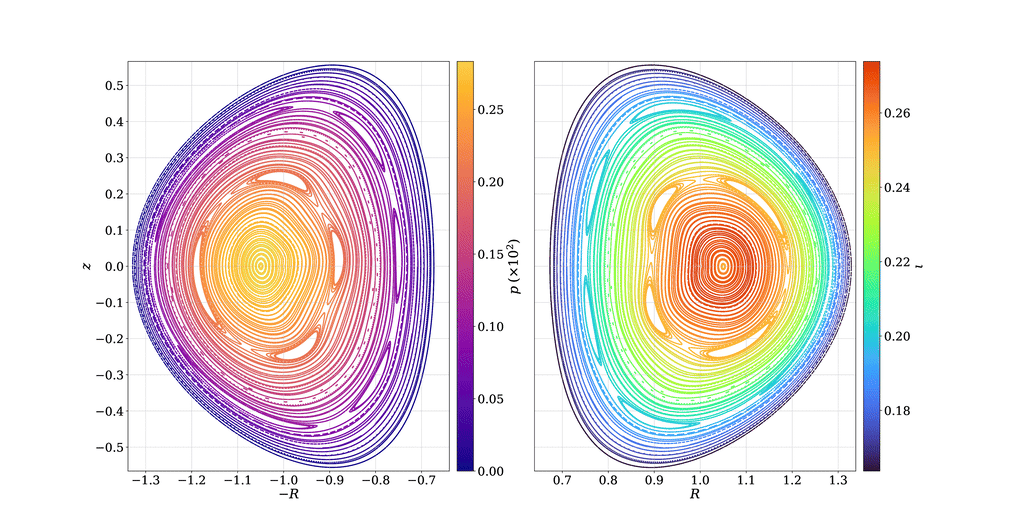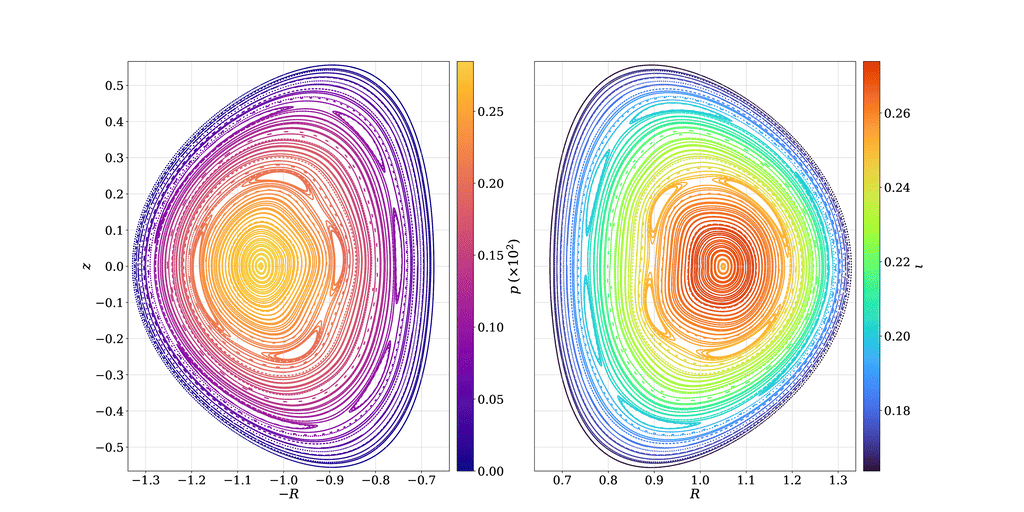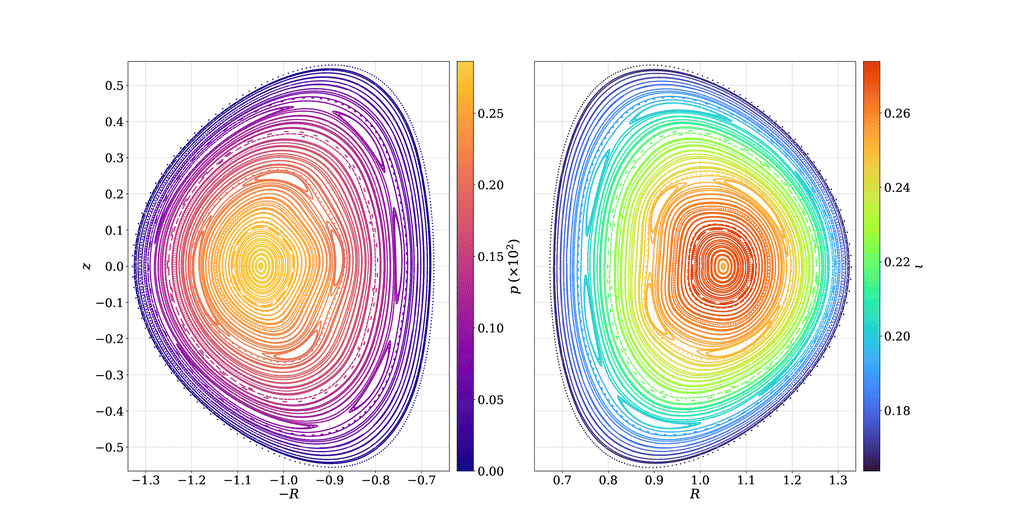
Magnetic relaxation with islands

Paper

MRX: A Differentiable 3D MHD Equilibrium Solver Without Nested Flux Surfaces
T. Blickhan, J. Stratton, A. A. Kaptanoglu
Submitted to Physical Review X

📄 Read on arXiv 📊 View Poster

Acknowledgements

This work was supported by the Simons Collaboration on Hidden Symmetries and Fusion Energy.