Reduced basis methods struggle with advection-dominated problems where solutions exhibit moving features (shocks, fronts, traveling waves). Standard linear approximation methods fail to capture these dynamics efficiently because the solution manifold has high Kolmogorov n-width.

We propose registration methods based on Optimal Transport that align solution snapshots before building the reduced basis, dramatically improving approximation quality.

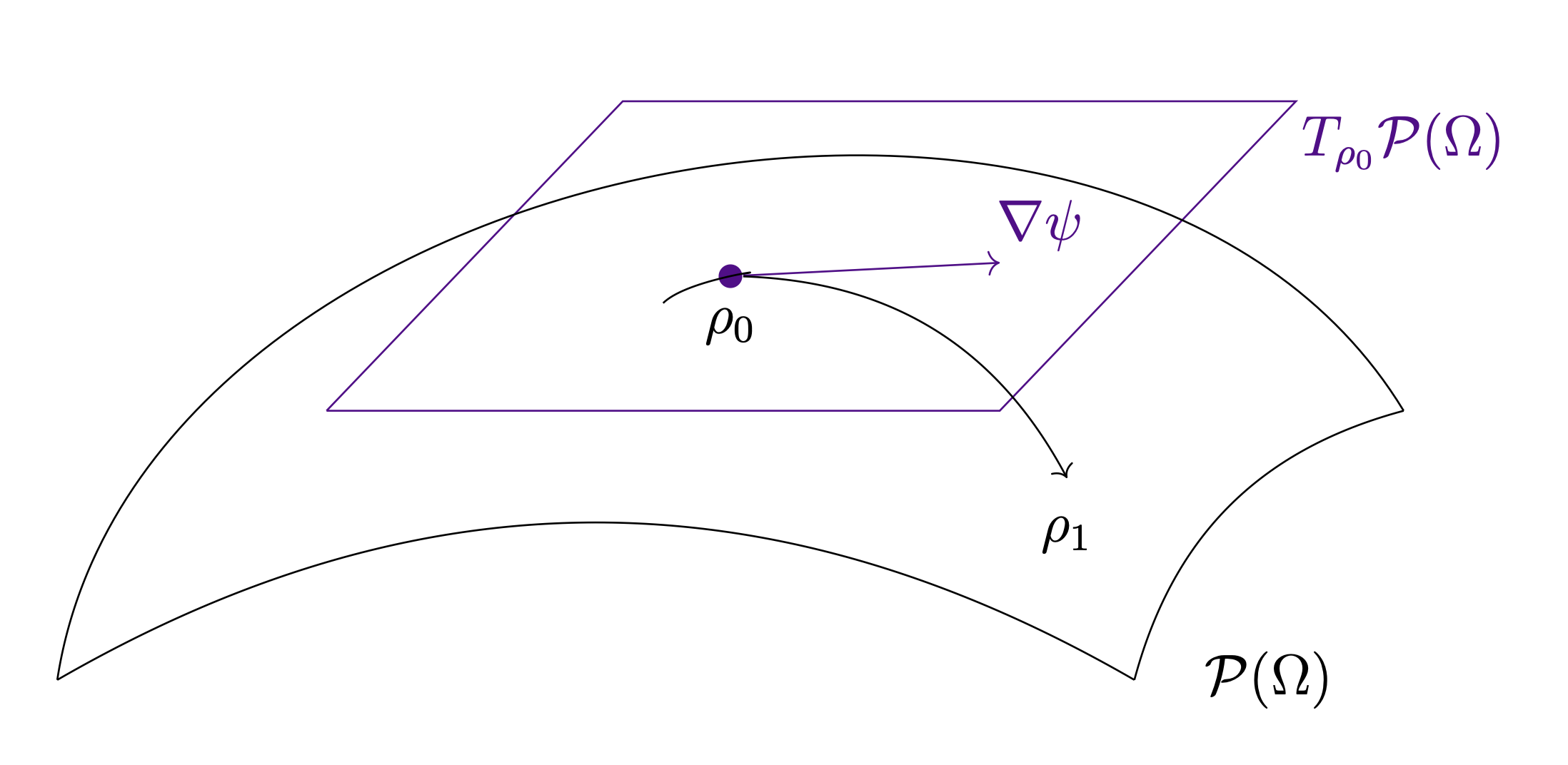
Given a reference measure $\mu_0$ and a family of measures $\mu_\theta$, $\theta \in \Theta$, the Monge embedding maps each $\mu_\theta$ to the optimal transport map $T_\theta$ pushing $\mu_0$ to $\mu_\theta$. These maps live in a linear space, allowing us to use linear reduction (i.e. POD) on the tangent space of the Wasserstein manifold. With that, we obtain a small set of transport modes that can be used to approximate new solutions.

Linear Optimal Transport

Papers

A Registration Method for Reduced Basis Problems Using Linear Optimal Transport

Tobias Blickhan SIAM Journal on Scientific Computing, 2024

📄 Paper

📄 arXiv

💻 Code

We provide a principled way to “align” solution snapshots, making them amenable to standard linear reduction techniques.

Wasserstein Model Reduction Approach for Parametrized Flow Problems in Porous Media

Beatrice Battisti, Tobias Blickhan, Guillaume Enchery, Virginie Ehrlacher, Damiano Lombardi, Olga Mula ESAIM: Proceedings and Surveys, 2023

📄 Paper

📄 arXiv

We develop Wasserstein barycenters and displacement interpolation for parametric flow problems.